The Basics

In machine learning, datasets typically produce two types of outputs: Regression and Classification.

• Regression outputs are continuous values.

• Classification outputs are discrete, often binary (e.g., 0 or 1).

For example:

• A regression task might predict housing prices in a locality, influenced by features like the number of bedrooms or floor space.

• A classification task could predict whether a person has a disease or not, with outputs such as positive or negative.

One versatile algorithm that works for both cases is K‑Nearest Neighbors (KNN). Its principle is straightforward: given a data point, KNN looks at its nearest neighbors and decides the output based on either majority voting (for classification) or averaging (for regression).

Lazy Learner

KNN is often called a lazy learner because it doesn’t build a model in advance. Instead, it simply stores the dataset and performs computation only when making predictions.

This has an advantage: input features can vary in dimension or scale, yet KNN can still distinguish between them because it relies on neighbor comparisons rather than memorizing patterns.

The Principle

KNN predictions are based on two approaches:

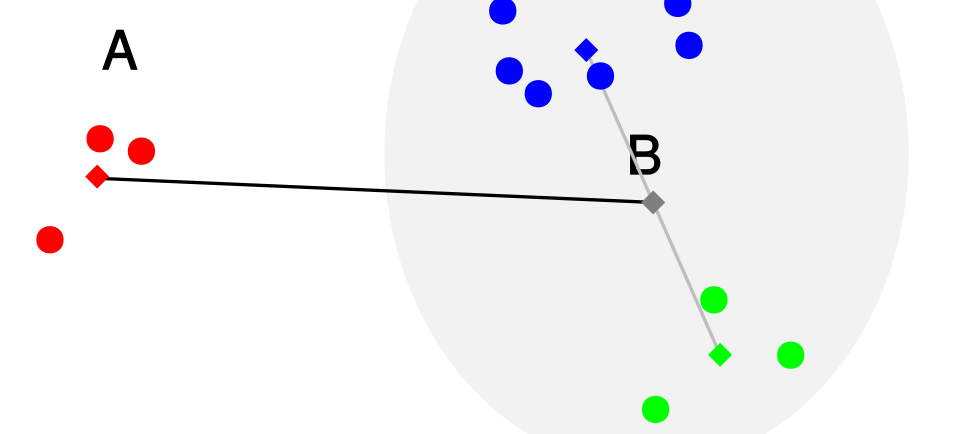
• Majority Voting (Classification): A data point is assigned to the class most common among its nearest neighbors. For example, if most neighbors belong to class A, the point is labeled as class A.

• Averaging (Regression): Instead of voting, the algorithm calculates the average of the nearest neighbors’ values. This average becomes the prediction.

The number of neighbors considered depends on the parameter K:

• If K = 3, the algorithm looks at the 3 closest neighbors and decides based on their majority class or average value.

• Choosing the right K is critical:

  • Small K: The model may over fit, performing well on training data but poorly on real-world data. (High variance, low bias)

  • Large K: The model may oversimplify, failing to capture important patterns. (High bias, low variance)

Distance Measurement

To find the “nearest” neighbors, KNN uses distance metrics:

• Euclidean Distance: The straight-line (shortest) distance between two points.

• Manhattan Distance: Distance measured along grid-like paths, similar to how a taxi navigates city blocks.

• Minkowski Distance: A generalization that combines Euclidean and Manhattan distances, offering more flexibility.

End Note

The K‑Nearest Neighbors algorithm is one of the simplest yet effective tools in machine learning. Its ability to handle both regression and classification tasks makes it a versatile choice for a wide range of scenarios.